Leonhard Euler tricentennial
This equation is considered one of the most beautiful equations in mathematics:
eiπ + 1 = 0.
When I taught high school, the chair of the department (who had a Master's Degree in mathematics from the University of Chicago, which is no mean feat) used the five numbers in this equation as her license plate. The equation is one of at least two equations known as Euler's equation; the other isV + F = E + 2.
Sunday (15 Apr 2007) is the tricentennial of Leonhard Euler's birthday. I've referred to Euler before as one of those mathematicians who lowers my mathematical self-esteem. Euler performed mental computations the way ordinary people breathe. He sometimes worked while one child played on one knee, and another child played on the other. He continued this habit of achieving magnificent heights in mathematics even after going blind in both eyes (not simultaneously). Consider that after he lost his sight in the first eye, he is reputed to have observed that he would now have less distraction.
He spent most of his career in Russia. This places him a little outside the geographic mainstream of the mathematics of the time. I've read that it has kept much of his unpublished work out of circulation. He remained there despite an offer by the university in Basel, his native canton in Switzerland, perhaps because Basel had refused to grant his wife citizenship. (Or Switzerland. One of the two; I find different information at different sources.)
Now, why should you care about Euler? Because most everything you use in daily life was engineered using mathematics that was studied and/or invented (or re-invented) by Euler. This could be said about Isaac Newton, too, since he invented Calculus (and Gottfried Leibniz later re-invented it), Euler changed the way people looked at Calculus, and helped to place it on more certain foundations.
Euler worked with the function e x, also called the exponential function. One can describe the meaning of this function very elegantly by this diagram:
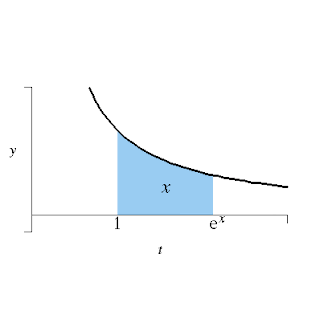
e x is the point on the x-axis such that the bluish area under the curve 1/t is x. For example, if you want the bluish region to have an area of 2, you locate its right border at e2.This function appears all over the sciences and engineering; for example, the computer you're using right now to read this depends on applications of this function.
Despite his accomplishments, Euler was known to be modest and quiet. When visiting Prussia, he was asked why he spoke so rarely, and replied famously, Madame, I have come from a country where one can be hanged for what one says.
In a less mathematical light, Euler was a deeply religious man, a literalist and a Calvinist at a time when Enlightenment thinkers insisted that Reason and Faith could not co-exist in the same mind. (This may remind you of the opinions of certain of our contemporaries.) He married and had thirteen children, although given the situation in those days, only five survived childhood.
So, go out to a restaurant on Sunday to celebrate the man's birthday! At least have a doughnut or something!








7 comments:
I shall have a snort of cognac and toast his name. I have great respect for mathamaticians, partly because I understand nothing of their arts.
You mentioned stay in Russia as being outside of the math geographic mainstream. That got me to thinking - is my impression that Indic civilization has always appreciated math and therefore produced its fair share of math geniuses correct? Or just a confused memory?
India has certainly produced a fair share of geniuses. One of them solved the quadratic equation (I mentioned this earlier) and there was of course Ramanujan. I know that many of the best American mathematicians are of Indic origin, and a few years ago it was an Indic couple of researchers who discovered a test for whether a number is prime that was polynomial-time. In all the hoopla over China's rise, India is getting unjustly ignored, or if not, it's is getting worse press than China.
But I don't know enough history of mathematics to say whether Indic civilization has "always" appreciated math. I have a vague feeling that they had their version of the dark age for a while, but this is the thought of an ignoramus who learns of such through reading Churchill's discussion of British colonization. I'm certainly not going to learn enough to correct that tonight (if it's wrong).
I do want to mention that by "being outside of the math geographic mainstream", I meant that the great Russian mathematicians who did exist in Tsarist times often didn't receive attention for their fantastic work. Lobachevsky is the example I have uppermost in mind. Chebyshev received attention, but at a talk I saw last week the speaker explained that Chebyshev didn't see himself as a "Russian" mathematician and did everything he could to move outside Russia. Sonya Kovalevskaya also had to travel outside Russia, but she was a woman which only complicated matters that much more. I've read that one reason so much of Euler's work is still to be discovered and unpublished is that he was in Russia, after all...
Thanks.
I too am ignorant about Indian history. I should check it out.
Someday.
I went through 4 Calculus courses and I don't believe I ever saw the area under the t^-1 curve trick. Very elegant.
--Joey
Joey, I went through fourt semesters of calculus, several more semesters of advanced calculus and analysis, to say nothing of algebra, and I never saw that trick, either!
What I saw is something similar in the Calculus book that we at USM. The author defines the natural logarithm as the area under the curve t^(-1) between t=1 and t=x. It was a snap to go from there to the definition of e^x as the position where you get an area of x.
What's best about it, though, is that it's probably the easiest explanation you can give to someone who knows no mathematics, even easier than the one about e^x having a tangent line whose slope is 1. With this definition, you don't need to know any jargon at all; you just draw a picture and talk about area and position, two highly intuitive concepts.
hi i am reasearching leonard euler and i want to know what country he moved to when he was 20
saeng,
I am not an expert on Leonhard Euler, but it looks as if that was when Euler moved to Russia.
Post a Comment